Toughness and resistance to brittle fracture

1. TOUGHNESS

Metals often show quite acceptable properties when small smooth bar specimens are tested in tension at ambient temperature and at slow loading rates. However, they fail in a brittle manner when large components are loaded or when the loading is performed at low temperatures or applied rapidly. Susceptibility to brittle fracture is enhanced if notches or other defects are present. Resistance to brittle fracture is commonly referred to as toughness.

Metals with a body-centred cubic lattice, e.g. pure iron and ferritic steels, have the characteristic that their fracture mechanism undergoes a dramatic transition with decreasing temperature from a tough ductile mode in the higher temperature region to a brittle cleavage mode at lower temperatures. Face-centred cubic metals, e.g. copper, aluminium, and austenitic steels, do not fail by cleavage under all loading conditions and at all temperatures.

1.1 Types of fracture

Ductile fracture involves the formation, growth, and coalescence of voids. A simple analogy is the fracture of plasticene or putty containing particles of sand. The voids form around precipitates or non-metallic inclusions (see Figure 1). The ductility or toughness of the material is basically dependent on the volume fraction of the void nucleating particles, i.e. the proportion of sand in the previous analogy. The amount of deformation prior to rupture and thus the toughness of the material increases with its purity.

The macroscopic orientation of a ductile fracture surface may vary from 90° to 45° to the direction of the applied stress. In thick sections, most of the fracture surface tends to be oriented at 90° to the direction of the applied tensile stress. However, ductile fractures commonly have a 'shear-tip' near a free boundary as the transverse stresses reduce to zero causing the plane of maximum shear to be at 45° to the direction of the applied stress.

Cleavage fracture occurs in body-centred cubic metals when the maximum principal stress exceeds a critical value, the so-called microscopic cleavage fracture stress .

Certain crystallographic planes of atoms are separated when the stress is sufficiently high to break atomic bonds. Crystallographic planes with low packing densities are preferred as cleavage planes. In steels, the preferred change planes are the bee cube planes.

The fracture surface lies perpendicular to the maximum principal stress and appears macroscopically flat and crystalline. When viewed by eye, a cleavage fracture usually displays characteristic chevron markings which point back to the origin of the fracture. When brittle fracture occurs in a large structure, such markings can be invaluable in identifying the site of crack initiation. When viewed under microscope, cleavage cracks can be seen to pass through the grains along preferred crystallographic planes (transgranular cleavage).

If grain boundaries are weakened by precipitates or by the enrichment of foreign atoms, cleavage cracks can also propagate along grain boundaries (intergranular cleavage).

1.2 Influence of temperature, loading rate, multi-axiality, and geometry

Temperature influences fracture behaviour mainly due to its effect on yield strength and the transition from ductile to cleavage fracture. Figure 2 shows schematically the yield strength and the microscopic cleavage fracture stress as a function of temperature for a ferritic steel. The yield strength falls with increasing temperature, whereas the cleavage fracture stress is hardly influenced. The transition temperature is defined by the intersection between the yield strength and cleavage fracture strength curves. At lower temperatures, specimens fail without previous plastic deformation (brittle fracture). Somewhat above the transition temperature, cleavage fracture can still occur due to the effect of deformation induced work hardening. At higher temperatures, cleavage is not possible, and the fracture becomes fully ductile.

The yield strength rises with increasing loading rate (marked with a dashed line in Figure 2), whereas the microscopic cleavage fracture stress shows almost no strain rate dependence. This rise causes the ductile-brittle transition temperature to move to higher values at higher rates of loading. Thus, an increase of loading rate and a reduction of temperature have the same adverse effect on toughness.

A multi-axial stress state has an important influence on the transition from ductile to cleavage fracture. A triaxial state of stress, in which the three principal stresses σ₁, σ₂, and σ₃ are all positive (but not equal), inhibits or constrains the onset of yielding. Under these conditions, yielding occurs at a higher stress than that observed in a uniaxial or biaxial state of stress. This situation is illustrated in Figure 3 where it can be seen that the transition temperature arising from the intersection of the cleavage and yield strength curves is shifted to a higher temperature, i.e. the metal has become more brittle.

The most familiar situation in which multi-axial states of stress are encountered in steel structures is in association with notches or cracks in thick sections. The stress concentration at the root of the notch gives rise to a local region of triaxial stresses even though the applied loading may be uni-directional (see Figure 4).

1.3 Notched impact bend test

The notched impact bend test is the most common test for the assessment of susceptibility to brittle fracture because it is inexpensive and quickly performed. 10mm square bars with a machined notch (ISO-V or Charpy specimens) are struck by a calibrated pendulum. The energy absorbed from the swinging pendulum during deformation and fracture of the test specimen is used as a measure of the impact energy. The notch impact energy consists of elastic and plastic deformation work, fracture energy, and kinetic energy of the broken pieces.

Figures 5 and 6 show the notch impact energy as a function of testing temperature. At low temperatures, the failure of ferritic steels occurs by cleavage fracture giving a lustrous crystalline appearance to the fracture surface. At high temperatures, failure occurs by ductile fracture after plastic deformation. In the transition range, small amounts of ductile fracture are found close to the notch but, due to the elevated stresses near the crack tip, the fracture mechanism changes to cleavage. Throughout the transition range the amount of cleavage fracture becomes less and the notch impact energy rises as the testing temperature increases. In Figure 6, T° are expressed in Kelvin (K) – equivalence is [°C] = [K] – 273.15.

In order to characterise the transition behaviour, a transition temperature is defined as the temperature at which:

• a defined value of the notch impact energy is reached (eg. T_27J, T_40J),
• half of the maximum impact energy value is reached (T_50%), or
• 50% ductile fracture is observed on the fracture surface (FATT 50: Fracture Appearance Transition Temperature, 50% ductile fracture).

The impact energy values obtained show a high amount of scatter in the transition area because here the results depend on the local situation ahead of the crack tip. Beyond this area, scatter becomes less because there is no change of fracture mechanism.

The notched impact bend test gives only a relative measure of toughness. This measure is adequate for defining different grades of toughness in structural steels and for specifying steels for well established conditions of service. For the assessment of known defects and for service situations where there is little experience of brittle fracture susceptibility, a quantitative measure of toughness which can be used by design engineers is provided by fracture mechanics.

1.4 Fracture toughness

Fracture mechanics provides a quantitative description of the resistance of a material to fracture. The fracture toughness is a material property which can be used to predict the behaviour of components containing cracks or sharp notches. The fracture toughness properties are obtained by tests on specimens containing deliberately introduced cracks or notches and subjected to prescribed loading conditions.

Depending on the strength of the material and the thickness of the section, either linear-elastic (LEFM) or elastic-plastic fracture mechanics (EPFM) concepts are applied.

The Linear-Elastic Fracture Mechanics Approach

The stress intensity factor K_I describes the intensity of the elastic crack tip stress field in a thick, deeply cracked specimen loaded perpendicular to the crack plane.

K_I = Y σ (1)

where

σ is the nominal stress

a is the crack depth

Y is the correction function dependent on the crack and test piece geometry

The critical value of the stress intensity factor for the onset of crack growth is the fracture toughness K_IC.

Another material property obtained from linear-elastic fracture mechanics is the energy release rate G_I. It indicates how much elastic strain energy becomes free during crack propagation. It is determined according to Equation (2):

G_I = Π Y² σ² a / E  = K₁² / E    (2)

where

E is the Young's modulus

Analogous to the stress intensity factor, crack growth occurs when G_I reaches a critical value G_Ic.

The fracture toughness properties K_Ic and G_Ic are determined with fracture mechanics specimens generally as shown in Figures 7 and 8.

The great value of the fracture toughness parameters K_Ic and G_Ic is that once they have been measured for a particular material, Equations (1) and (2) can be used to make quantitative predictions of the size of defect necessary to cause a brittle fracture for a given stress or the stress which will precipitate a brittle fracture for a defect of known size.

As the designation implies, linear elastic fracture mechanics is applicable to materials which fracture under elastic conditions of loading. The fracture phenomena in high strength quenched and tempered steels are of this type. In lower strength structural steels, extensive plasticity develops at the notch root before failure occurs. This behaviour invalidates many of the assumptions of linear elastic fracture mechanics and makes testing difficult or not meaningful. In such cases, elastic-plastic fracture mechanics must be applied.

There are two alternative techniques of elastic-plastic fracture mechanics:

1. Crack tip opening displacement (CTOD)
2. J-integral

Their essential features are summarised below.

The elastic-plastic fracture mechanics approach

A consequence of plasticity developing at the tip of a previously sharp crack is that the crack will blunt and there will be an opening displacement at the position of the original crack tip. This is the crack tip opening displacement (CTOD). As loading continues, the CTOD value increases until eventually a critical value d_c is attained at which crack growth occurs.

The critical crack tip opening displacement is a measure of the resistance of the material to fracture, i.e. it is an alternative measurement of fracture toughness.

For materials which exhibit little plasticity prior to failure, the critical CTOD, δ_c, can be related to the linear elastic fracture toughness parameters K_Ic and G_Ic as follows:

K_Ic² = E.G_k / (1 - υ²) =  m.E.σ_y.δ_c / (1 - u²)   

where

E is Youngs modulus

σ_y is the uniaxial yield strength

u is Poisson's ratio

m is a constraint factor having a value between 1 and 3 depending on the state of stress at the crack tip.

Another way of taking account of crack tip plasticity is the determination of the J-integral. J is defined as a path-independent line-integral through the material surrounding the crack tip. It is given by:

where

U is the potential energy

B is the specimen thickness

a is the crack length

U = 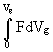(4)

F is the load

V_g is the total displacement

Since the determination of J is difficult, approximate solutions are used in practice.

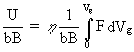
where

b = w - a

η = 2 (for SENB-specimens)

η = 2 + 0.522 b/w (for CT-specimens)

The critical value of J is a material characteristic and is denoted J_Ic. For the linear elastic case, J_Ic is equal to G_Ic.

1.5 Fitness for purpose

Conventional assessment of components is based on a comparison of design resistance with applied actions. Toughness criteria are generally satisfied by the appropriate selection of material quality. However, there are situations where a more fundamental assessment has to be carried out because of:

• service conditions
• defects during manufacture
• defects, e.g. fatigue cracks, developing during previous service life

Such assessments can be performed by different methods. If the component is small, it may be possible to test it. For large or unique structures, such as bridges or offshore platforms, this method of producing the most realistic data has to be excluded. Tests on representative details of a component may be performed if the simulation of the real structure is done carefully, e.g. accounting for specific service conditions including the geometry of the structure and discontinuities, loading rate, service temperature, and environmental conditions. A typical example of such a test method is the wide plate test, which is discussed below.

Fracture mechanics concepts have been developed to assess the safety of components containing cracks. Depending on the overall behaviour of the component (linear-elastic or elastic-plastic), different methods can be used for failure assessment.

1.5.1 Wide plate testing

Over the last decades, large flat tensile specimens, so-called wide plates, have been used to simulate a relatively simple detail of a tension-loaded large structure. A main objective of wide plate testing is the evaluation of the deformation and fracture behaviour of a specimen under service conditions. The second reason for this kind of test is the application of test results for the development and checking of failure assessment methods, e.g. fracture mechanics methods.

Wide plate tests require testing facilities with high loading capacities due to the fact that such tests are usually carried out at full thickness. The maximum dimensions of wide plates tested on large test rigs with a load capacity of up to 100MN are as follows:

• specimen width W ≤ 3000mm
• specimen thickness to ≤ 300mm
• specimen length l ≤ 5000mm

Figure 9 shows different types of specimen containing discontinuities for tests on the base metal or welded joints. The discontinuities may be through-thickness or surface notches or cracks. The configuration of the plate is usually chosen according to the specific structural situation to be assessed.

Stress or strain criteria can be used as safety criteria which must be fulfilled to assure the safety of a specific structural element. The production of a given amount of overall strain is in some cases used as the failure criterion. The gross-section-yielding concept requires that gross-section-yielding (GSY) occurs prior to fracture. Based on this concept, wide plates with different crack lengths are tested under similar loading conditions to determine a critical crack length just fulfilling the GSY-criterion. Figure 10 shows the ratio of the maximum gross-section stress in the structure to ultimate tensile strength as a function of the crack length ratio 2a/W of centre-notched wide plates. The upper limit line describes the theoretical maximum stress if the ultimate tensile strength is reached in the cross-section containing the discontinuity. All test results show lower values than are implied by the theoretical line, resulting from the important influence of toughness in the presence of discontinuities. Only in the case of infinite toughness can the theoretical line be reached. The intersection of the experimentally determined curve and the yield strength line marks the critical crack length ratio 2a_c/W. As long as the 2a/W ratio is smaller than the critical ratio, the GSY-criterion is fulfilled. Unfortunately, the critical 2a_c/W ratio depends strongly on the dimensions of the crack and the plate so that different types of cracked components always require a series of specific wide plate tests. This concept is therefore only used if other concepts cannot be applied.

1.5.2 Fracture mechanics concepts

The basis of a fracture mechanics safety analysis is the comparison between the crack driving force in a structure and the fracture toughness of the material evaluated in small scale tests. The application of one of the concepts depends on the overall behaviour of the structure which may be linear-elastic (K-concept) or elastic-plastic (CTOD- or J-integral concepts). For a safe structure, the crack driving force must be less than the fracture toughness. In general, the toughness values of the material are evaluated according to existing standards. The crack driving force can be calculated on the basis of analytical solutions (K-concept), empirical, or semi-empirical approaches (CTOD-Design-Curve approach, CEGB-R6-procedures) or using numerical solutions (indirectly: EPRI-handbook, directly: finite-element calculations). The different methods are explained briefly below:

• K-concept

The K-concept can be applied in the case of linear-elastic component behaviour. The crack driving force, the so-called stress intensity factor K_I, defined in Section 1.4, has been evaluated for a large range of situations and calculation formulae are, for example, given in the stress-analysis-of-cracks handbook.

Usually, the critical fracture toughness K_Ic of the material is evaluated according to the EN ISO 12135 - 2021. Brittle failure can be excluded as long as:

K_I < K_Ic

For a given fracture toughness, the critical crack length or stress level can be calculated from:

• CTOD-Design-Curve approach

A critical crack length or stress level can be determined using the limit curve of the CTOD-Design-Curve approach for the driving force assessment together with measured values of CTOD_crit for the material. The latest version of the limit curve is shown in Figure 11 and can be used for:

2a/W ≤ 0.5 and σ_net ≤£ σ_YS.

 

Analysis can only be performed under global elastic conditions (σ_net ≤ σ_YS) although local plastic deformation may occur in front of a crack tip which is accounted for in the CTOD-value of the material.

• CEGB-R6-routines

The CEGB-R6-routines can be used to assess the safety of structures for brittle and ductile component behaviour. The transition from linear-elastic to elastic-plastic behaviour is described by a limit curve in a failure analysis diagram (see Figure 12). The ordinate value K_r can be regarded as any of three equivalent ratios of applied crack driving force to material fracture toughness as follows:

• Other methods

Other methods have emered. The Electrical Power Research Institute (EPRI) in New York has used a detailed analysis by finite elements to determine limiting J contour values for standard geometries. Alternatively, the J contour values may be obtained by direct finite element analysis of the particular situation.

Read more